
Mein Beitrag ‚Einen Kegel konstruieren‘ war erheblich zu wortreich ;-), darum habe ich einen Online Kegelrechner geschrieben.
Hinweis: Leider funktioniert der Online Kegelrechner anscheinend nicht unter allen Umständen und ich habe einfach keine Zeit, mich da durchzukämpfen, darum schreibe ich die Formel für alle Fälle noch einmal dahinter.
Hm, Du hast Javascript ausgeschaltet, was bedeutet, dass der Online Kegelrechner sowieso nicht funktioniert.
Du hast jetzt 2 Möglichkeiten:
- Javascript einschalten oder
- den Kegel nach der folgenden Formel selbst berechnen.
|
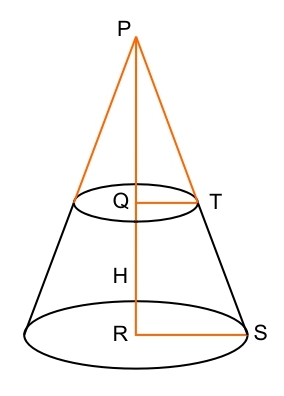
Der schwarze Kegel in der Grafik ist das, was wir erreichen möchten. kleiner Durchmesser = kleinerer gewünschter Durchmesser grosser Durchmesser = größerer gewünschter Durchmesser Höhe = gewünschte Höhe |
|
|
QT = kleiner Durchmesser / 2 RS = grosser Durchmesser / 2 PQ = QT * Höhe / (RS – QT) PR = PQ + Höhe PT = √((PQ * PQ) + (QT * QT)); Winkel zum Wegschneiden = Innerer Kreisdurchmesser = 2 * PT; |
|
Weiter geht’s:
Zeichne zwei zentrierte Kreise mit dem inneren und dem äusseren Kreisdurchmesser, zeichne den ermittelten Winkel ein und schneide ihn weg.
Das Ergebnis sollte eine Vorlage für einen Kegel mit den von Dir gewünschten Massen sein ;-)
Wer kein Geodreieck hat, kann die Gradscheibe von dem Beitrag ‚Einen Kegel konstruieren‘ ausdrucken und ausschneiden.
Wenn Du genauer wissen möchtest, was Du da eigentlich tust, dann guck‘ Dir doch noch einmal den Beitrag ‚Einen Kegel konstruieren‘ an ;-)
Links:
Hier bei unikatissima: ‚Einen Kegel konstruieren‘
genau das hab ich gesucht, meine Mathe-kenntnisse waren einfach zu lange her. super!
munich,
sag’s nicht weiter, aber mir ging’s mit dem „einfach zu lange her“ genauso ;-)
Schön, dass ich helfen konnte! :)
Hallo Susanne,
schön, dass es heutzutage noch Menschen gibt, die sich auch mit den „unwichtigeren“ Dingen des Lebens befassen und dieses Wissen auch noch mit anderen teilen!
Dein Artikel mit Formel hat mir sehr geholfen, danke!
MfG
Gernot aus Österreich
Gernot,
schön, dass ich helfen konnte :)
Und ich persönlich finde die Berechnung eines Kegels nicht wirklich unwichtig – manchmal braucht man einfach einen Kegel ;-)