Addendum: This entry is a little longish, if you only want to get the formula, check out the entry ‘Online Cone Calculator’.
Many crafters reach somewhen a point when they need a template for a truncated cone, be it to make cone-shaped lamp shades from patterned vellum, be it for a part of a clown costume for the child, a template for a piece of jewelry from metal or polymer clay or to make a papermaché vase.
I think that most then have a clear idea about the upper and bottom diameter and the height of the cone.

Additionally we know then that the template for the cone must be in a similar shape than one of those besides.
But how to get from the height and the diameters to the template that really makes the desired cone?
I recently pondered on this question and found math central.
There you can ask questions and check the answers to questions already put.
There are several answers to the topic ‘cone’ (simply enter cone’ into the search box) and I tried to compile from the answers a really simple instruction on how to construct cones.
It seems to be a little complicated when reading it first, but if you strictly follow the instructions, it isn’t hard. Admittedly most of us will need a calculator, because we will need later the square root of a value.
I interspersed some basic knowledge in between, because I had to re-collect tediously everything I have learned ages ago and I have completely forgotten ;-)
And I tagged the actual formulas with a  at the beginning.
at the beginning.
Have fun with it!
 (Click picture to enlarge)
(Click picture to enlarge)
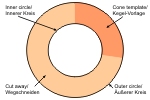
First of all: what does a cone template consists of?
On the picture on the left you see, that our template consists of an outer and an inner circle and (light orange) a piece that we have to cut away.
First we will fix the sizes of our circles and later how much we have to cut away.
To this end we first identify the diameters of both of our circles for our cone template.
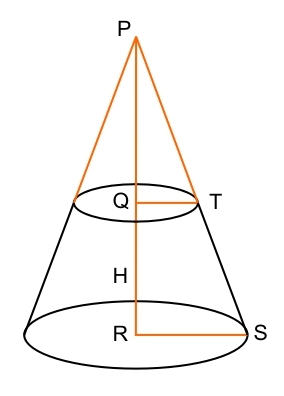
If you look at the diagram (I’ve been geared to a diagram of math central) you see, that both distances PT and PS equate the half of the diameters of our both circles from above.
(If you haven’t understand this, it doesn’t matter, simply go on.)
Therefore we will calculate PT and PS.
We will call the height H, the diameter at the top DiaT and the diameter at the bottom DiaB.
We need the desired radiuses for the formula.
That’s easy because the radius is exactly the half of the desired diameter.
Let’s call the radius at the top Rt and at the bottom Rb.
Let’s see a concrete example: our cone (that’s the one from the photo at the top) should have a height of 7cm, a diameter at the top of 3cm and a diameter at the bottom of 7cm.
Caution: All units must always be the same: they are all mm, or cm or m ;-)
 H = QR = 7
H = QR = 7
DiaT = 3
DiaB = 7
Because a radius always equals the half of a diameter, we know additionally:
 Rt = QT = 1,5
Rt = QT = 1,5
 Rb = RS = 3,5
Rb = RS = 3,5
Now we need the distances PQ and PR that we must calculate (I found the formula in an answer of math central):
 PQ = Rt * H / (Rb – Rt)
PQ = Rt * H / (Rb – Rt)
This is in our example PQ = 1,5 * 7 / (3,5 – 1,5) = 5,25
 PR = PQ + H
PR = PQ + H
This is in our example PR = 5,25 + 7 = 12,25
The formulas for PT and PS are as follows:
 PT = sqrt(PQ2 + QT2) = sqrt((PQ * PQ) + (QT * QT))
PT = sqrt(PQ2 + QT2) = sqrt((PQ * PQ) + (QT * QT))
 PS = sqrt(PR2 + RS2) = sqrt((PR * PR) + (RS * RS))
PS = sqrt(PR2 + RS2) = sqrt((PR * PR) + (RS * RS))
Note: ‘sqrt’ means ‘square root’ (symbol: √).
Personally I don’t know how to extract a root (except for 9 perhaps ;-))), but every calculator provides this function and all computers have a calculator (somewhere!) ;-))
Let’s continue our example:
PT = sqrt((5,25 * 5,25) + (1,5 * 1,5)) = sqrt(27,5625 + 2,25) = sqrt(29,8125) = 5,5
PS = sqrt((12,25 * 12,25) + (3,5 * 3,5)) = sqrt(150,0625 + 12,25) = sqrt(162,3125) = 12,7
Note: In our example one decimal place is fully satisfying, and I’m rounding off up to 5 and up above 5.
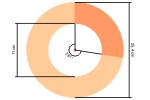
Well, now we know that our outer circle has a diameter of 2 * PS = 25,4 and our inner circle a diameter of 2 * PT = 11.
We calculated everything in cm, therefore we have now 25,4cm and 11cm.
Now we can go on finding out how much we must cut away from our ring.
Luckily we don’t have to think too much, because there’s a ready-made formula (that I also found at mathcentral):
We calculate the angel a which identifies the area that we don’t(!) need as follows:
 a = 360 * (1 – ((2 * π * Rb) / (2 * π * PS)))
a = 360 * (1 – ((2 * π * Rb) / (2 * π * PS)))
Note: π means ‘Pi’ and I’m using 3,14 although the number goes on forever.
For accuracy fanatics ;-): these are the first 100 decimal places of Pi: 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… ;-)
Let’s continue our calculation.
We thus calculate the angle a as follows:
a = 360 * (1 – ((2 * π * 3,5) / (2 * π * 12,7))) = 360 * (1 – (21,991 / 79,796)
= 360 * (1 – 0,276) = 360 * 0,724 = 260,64 which is approximately 261°
 (Click picture to enlarge)
(Click picture to enlarge)
Great!
And what do we do now with the calculated degrees?
We cut them away ;-)
 (Click picture to enlarge)
(Click picture to enlarge)
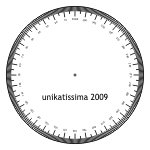
If you don’t have a protractor you can print and cut the degrees disk.
Put the disk exactly centered into the ring and draw straight lines with a ruler from the center to the 0/360° label and (in our example) from the center to the 261° label.
The lines look then like the dotted lines on the previous picture and mark the area we have to cut away.
 Note: I suggest to construct the cone template first with news paper or scrap paper.
Note: I suggest to construct the cone template first with news paper or scrap paper.
To find the center you can then simply half fold the uncut circles twice (see the photo). Then it will be easy to place the protractor correctly.
Links:
At math central (English, French, Spanish):
 List of already answered questions
List of already answered questions
 Form to ask a question
Form to ask a question
 Search form
Search form
 Answer for the question with the subject: ‘Constructing a cone’
Answer for the question with the subject: ‘Constructing a cone’
 Answer for the question with the subject: ‘Pattern for a truncated cone’
Answer for the question with the subject: ‘Pattern for a truncated cone’
At Wikipedia (German): The first 100 decimal places of Pi (Die ersten 100 Nachkommastellen von Pi)
At Wikipedia (English): The first 50 decimal places of Pi
Here at unikatissima:
 Entries with the tag ‘fimo’
Entries with the tag ‘fimo’
 Entries with the tag ‘paper mache’
Entries with the tag ‘paper mache’

thank you very much very very very much
its weird i didnt found this page before
was so easy to explain ,besides months ago
when i was making the 1st steps of searching the trunckd cone template,
the formulas were very very hard to understand
cause the person was using integrals and derivades
i said WHAT? is that hard
you prove it it is not thks i will do the template tomorrow
see if it works
I’m glad that you like it :)
thank a lot this will be usefull for my lamps making
jacko,
I wish you good success! :)
My spouse and I absolutely love your blog and find nearly all of your post’s to be what precisely I’m looking for. Does one offer guest writers to write content for yourself? I wouldn’t mind composing a post or elaborating on a number of the subjects you write with regards to here. Again, awesome site!
Thank you for your compliments! :))
And also thank you for your offer to write entries, but that’s not necessary.
On the other side I’m always grateful for hints onto where to find new (free) tutorials for interesting crafts, although I can’t promise to use them.
Enjoy your crafting!
Its like you learn my thoughts! You appear to understand so much about this, like you wrote the e-book in it or something. I feel that you just can do with some percent to force the message house a bit, however other than that, that is great blog. A fantastic read. I will definitely be back.
Whatever is to be a hook, bends early. – German Proverb